[最新] f(x)=x^2 1 is bijective 320774-F(x)=x^2+1 is bijective

In mathematics, injections, surjections, and bijections are classes of functions distinguished by the manner in which arguments (input expressions from the domain) and images (output expressions from the codomain) are related or mapped to each other A function maps elements from its domain to elements in its codomain Given a function f X → Y {\displaystyle f\colon X\to Y} The functionF(x) = 1 e x Theorem 271 If a function is a bijection, then its inverse is also a bijection Proof Let f A!e a bijection and let f 1 B!Abe its inverse To show f 1 is a bijection we must show it is an injection and a surjection Let x 1;x 2 2e such that f 1(x 1) = f 1(x 2) Then by the de nition of the inverse we have x 1 = f(f 1(x Ex 12, 10 Let A = R − {3} and B = R − {1} Consider the function f A → B defined by f (x) = ((x − 2)/(x − 3)) Is f oneone and onto?

Determine Whether The Function F Z Z F X 4x Is Chegg Com

F(x)=x^2+1 is bijective

F(x)=x^2+1 is bijective-  199 Suppose I want to prove that the function f (0, \infty) \to (0, \infty) defined by f (x) = x^2 is bijective Let a, b \in (0, \infty)Definition 21 Let f X → Y be a function We say f is onto, or surjective, if and only if for any y ∈ Y, there exists some x ∈ X such that y = f(x) Symbolically, f X → Y is surjective ⇐⇒ ∀y ∈ Y,∃x ∈ Xf(x) = y To show that a function is onto when the codomain is a finite set is

State Whether The Function F R R Defined By F X 1 X 2 Is One One Onto Or Bijective

A) f(x) = 2x1 Bijective This is injective because for every a 6= b, we have f(a) 6= f(b) (every number is 1 more than 2 times some number) We also know that the function is surjective because the range is all real numbers from 2((y 1)=2)1 = y b) f(x) = x2 1 Not injective and not surjective We know the function is not injective because weLet A = R − (2) and B = R − (1) If f A B is a function defined by`"f(x)"=("x"1)/("x"2),` how that f is oneone and onto Hence, find f −1For f X → Y and g Y → Z functions, prove items 2), 3), 4) from page 123 of lecture notes (a) f and g surjective implies that g f is surjective (b) f and g bijective implies that g f is bijective (c) g f injective implies that f is injective Problem 4

Get an answer for 'show that f(x)=x^21 is a bijection x in (1, inf) y in (2,inf)' and find homework help for other Math questions at eNotesTo understand a bijection, you need to understand 2, simpler concepts Injection and Surjection Let mathf/math be a function with domain A, and codomain B Injection means that every element in A maps to a unique element in B That is to say,Functions can be injections (onetoone functions), surjections (onto functions) or bijections (both onetoone and onto) Informally, an injection has each output mapped to by at most one input, a surjection includes the entire possible range in the output, and a bijection has both conditions be true This concept allows for comparisons between cardinalities of sets, in proofs comparing the

The function f is onto if there x ∈ A such that f (x)= y ∴ f is onto Since f is one=one and onto then, the given function is bijectiveGiven that f(x) = x/(1 x^{2}) Taking the derivative of f(x) we get f'(x) = (1 x^{2} 2x^{2})/ (1x^{2})^{2}= (1x^{2})/(1x^{2})^{2} = since for all real x, 1Next, let y = 1 There is no x 2Z such that x2 4x 4 = 1 (since x2 4x 4 = (x 2)2) Therefore, h is not surjective 4 Prove that the function f Rf 1g!Rf 1gde ned by f(x) = x 1 x 1 3 is bijective Solution Side work To show that f is surjective, we need to show that for any y 2Rf 1g, we can nd an x such that x 1 x 1 3 = y Take the cube

F R R Given By F X X Sqrt X 2 Is A Injective B Surjective C Bijective D None Of These

What Is The Inverse Of The Function F X X X 1 Quora

So, the element "9" of the ring Z(26) is inverse to the element "3" It is the answer to question (a)Is f(x) = x e^(x^2) injective?Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music

Example 10 Show F 1 F 2 1 And F X X 1 Is Onto

Ex 1 2 2 I Check The Injectivity And Surjectivity Of F N N

Example 462 The functions f R → R and g R → R (where R denotes the positive real numbers) given by f(x) = x5 and g(x) = 5x are bijections Example 463 For any set A, the identity function iA is a bijection Definition 464 If f A → B and g B → A are functions, we say g is an inverse to f (and f is an inverse to g) ifAlternatively, f is bijective if it is a onetoone correspondence between those sets, in other words both injective and surjective Example The function f(x) = x2 from the set of positive real numbers to positive real numbers is both injective and surjective Thus it is also bijectiveThe map f x > 3x b is the bijective for any "b", because 3 mod 26 is an invertible element of the ring Z(26) Indeed, in this ring 3*9 = 1 (since 3*9 = 27 = 1 mod 26);

Show That A Function F R R Given By F X Ax B A B R A 0 Is A Bijective Sarthaks Econnect Largest Online Education Community

Let A X Xepsilonr F Is Defined From Ararrr As F X 2x X 1 Then F X Is A Surjective But Nor Injective B Injective But Nor Surjective C Neither Injective Surjective D Injective

 Let \(f 0, α) → 0, α) \) be defined as \(y = f(x) = x^2\) Is it an invertible function?The map ginduces a bijective continuous map f X !Z, which is a homeomorphism if and only if gis a quotient map 2 If Zis Hausdor , so is X 3 Closure, Interior, and Limit Points De nition 13 A subset Aof a topological space Xis closed if the set X Ais open Theorem 11 Let Xbe a topological spaceFor all x 1, x 2 ∈ X In addition, if T , S are bijective jointly separating maps such that T − 1, S − 1 Y → X are jointly separating, then T , S are called jointly bisep arating maps 3

Renethajb Files Wordpress Com 19 09 1 Function Dcs Part 3 Discrete Module 1 Cs 1 Pdf

How To Prove The Rational Function F X 1 X 2 Is Surjective Onto Using The Definition Youtube

Y = f (x) = x−2 x−3, ⇒ x− 2 = y(x−3), ⇒ x−2 = xy−3y, ⇒ xy−x = 3y−2, ⇒ x(y−1) = 3y−2, ⇒ x = 3y−2 y−1 As you can see, the preimage x exists for any y ≠ 1 Consequently, the function f is surjective and, hence, it is bijective The inverse function f −1 is expressed as x = f −1(y) = 3y−2 y−1State whether the function fR→Rdefined by f(x)=1x2is oneone onto or bijective Medium Open in App Solution Verified by Toppr Given, function fR→Rsuch that f(x)=1x2, Let A and B be two sets of real numbers Let x1 ,x2 ∈Asuch that f(x1 )=f(x2 ) ⇒1x12 =1//googl/JQ8NysHow to Prove the Rational Function f(x) = 1/(x 2) is Surjective(Onto) using the Definition

12 Determine Whether Each Of The Following Are Chegg Com

Injective Function Wikipedia

 Raji visited the Exhibition along with her family The Exhibition had a huge swing, which attracted many children Raji found that the swing traced the path of a Parabola as given by y = x 2 Answer the following questions using the above informationConsider f R{4/3} implies R{4/3} given by f(x)= 4x3/3x4 show that f is bijective find the inverse of f and hence find f^1(0) and x such that f^1(x)=2;Find the domain range of f(x)= 2(sinx)^23sinx4 what is symmetric relation

Prove That The Function F Nvecn Defined By F X X 2 X 1 Is One One But Not Onto Youtube

How To Determine If A Function Is One To One Mathematics Stack Exchange

 And further, $$ f'(x) = 1 frac1{1x^2}gt 0 quadforall x inmathbb{R}$$ Therefore the function is strictly increasing and hence, is strictly monotonic Therefore this function is bijectiveExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicQuestion (6 marks) Give a careful proof that the function f R\ {3} → R \ {1} given by f(x) = x 2 X – 3 is bijective This problem has been solved!

Let F R Rightarrow R Be Given By F X X 2 3 And Chegg Com

Question 13 Determine Whether Each Of These Chegg Com

 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange 965 Yes, that is correct and shows that, because f is injective, so is To show that is surjective, you want to prove that, for any x in X, there exist y in Y such that Given any x in X, let y= f (x) Then use the other direction #5The linear transformation f is O injective surjective bijective none of these c If f is bijective, find the matrix of its inverse If f is not bijective, enter DNE in every answer blank f'(x, Question 2 (1 point) Let f R2 → R2 be the linear transformation defined by f(x, y) = (5x – y, x – 5y) a

Let A R 2 B R 1 If F A B Is A Function Defined By F X X 1 X 2 Show That F Is One One Onto Sarthaks Econnect Largest Online Education Community

Determine With Justification Whether The Following Chegg Com

Define superposition principle briefly and its derivation;Graph f(x)=(x1)^22 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focus(a) Injective if for all x1,x2 ∈X, f(x1) = f(x2) implies x1 = x2 (b) Surjective if for all y∈Y, there is an x∈X such that f(x) = y (c) Bijective if it is injective and surjective Intuitively, a function is injective if different inputs give different outputs The older terminology for "injective" was "onetoone"

Determine Whether Each Of These Functions Is A Chegg Com

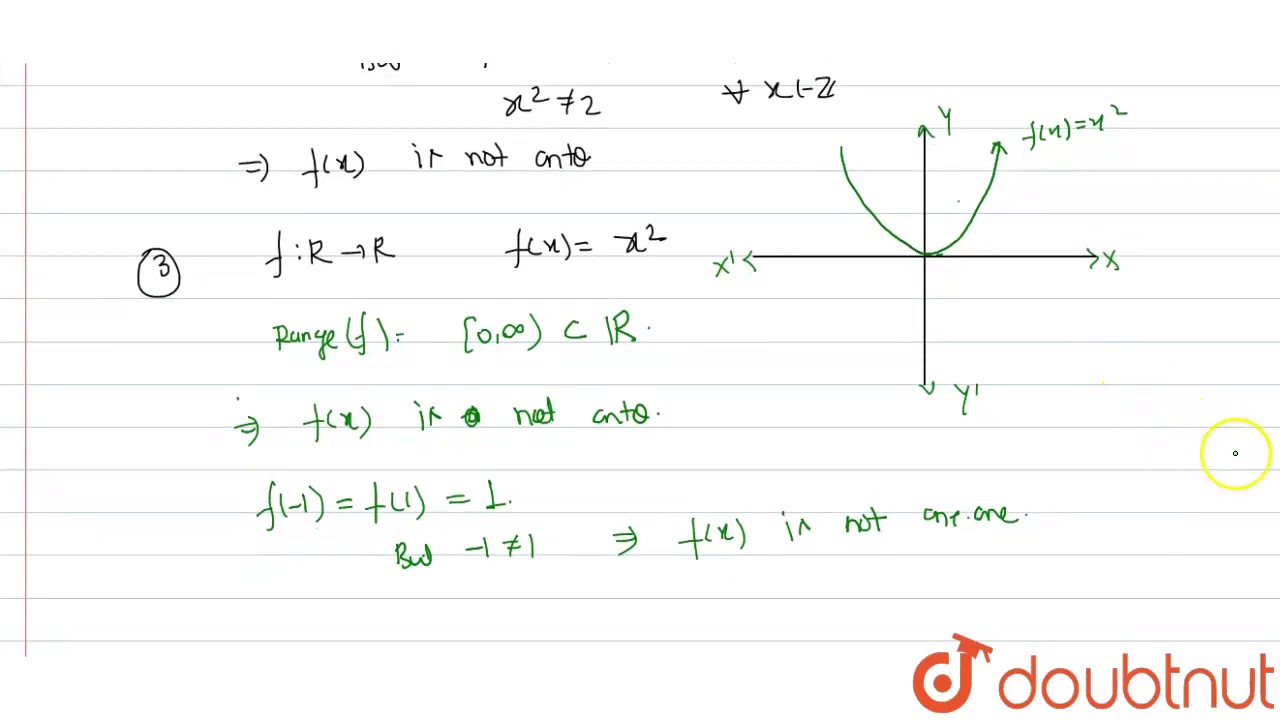
Show That The Function F R R Defined As F X X 2 Is Neither One One Nor Onto

The function f 3(x) = ex from set R to set R is surjective Take any positive real number y The preimage of this number is equal to x = lny, since f 3(x) = f 3(lny) = elny = y Thus, the function f 3 is surjective, and hence, it is bijective If we take x1 = −1 and x2 = 1, we see that f 4(−1) = f 4(1 let A=R {3} , B=R {1} If f AB be defined by f (x)= x2/x3, & all x EA Show that f is Brainlyin Let A=R {3} , B=R {1} If f AB be defined by f (x)= x2/x3, & all x EA Show that f is bijective See what the community says and unlock a Putting f (x1) = f (x2) we have to prove x1 = x2 Since x1 & x2 are natural numbers, they are always positive Hence, x1 = x2 Hence, it is oneone (injective) Check onto (surjective) f (x) = x2 Let f (x) = y , such that y ∈ N x2 = y x = ±√𝑦 Putting y = 2 x = √2 = 141 Since x is not a natural number Given function f is not onto So, f is not onto (not surjective)

Check The Injectivity And Surjectivity Of The Following Functions I F N N Given By F X X 2 Ii F Z Z Given By F X X 2 Iii F R

How To Prove That F R R F X 2x 3 Is Bijective Quora

 Thus, f is bijective Option C f (x) = 2x 1 Let f(x 1) = f(x 2) ⇒ 2x 1 1 = 2x 2 1 ⇒ x 1 = x 2 ⇒ f is one one Let f(x) = y, y ∈ Z ⇒ y = 2x 1 ⇒ y 1 = 2x ⇒ x = (y 1)/2 We observe that if we put y=0, then Thus, y = 0 ∈ Z does not have pre image in Z (domain) ⇒ f is not onto Thus, f is not bijective Option D f (xAlgebra Find the Domain and Range f (x)=x^21 f (x) = x2 1 f ( x) = x 2 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationLet fR\rightarrow R be defined by f (x)=2x6 which is a bijective Filo Class 12 Math Calculus Relations and Functions II 507 150 Let f R → R be defined by f (x) = 2x 6 which is a bijective mapping then f −1(x) is given by 2x

Cs100 Discrete Structures Ppt Download

Soni Matrix Match Type 28 Match The Functions Given In Column I Correctly With Mappings Given

When we subtract 1 from a real number and the result is divided by 2, again it is a real number For every real number of y, there is a real number x So, range of f (x) is equal to codomain It is onto function Hence it is bijective function (ii) f R > R defined by f (x) = 3 – 4x 2 SolutionIf so find its inverse Solution Yes, it is an invertible function because this is a bijection function Its graph is shown in the figure given below Let y = x 2 (say f(x)) \(\Rightarrow x = \sqrt{y}\) But x can be positive, as domain of f is 0, α) We have 2 random variables X and Y and Y is a function of X, f(X) It seems obvious that H(XY) = 0 = H(YX) if f(X) is a bijective function, as there is an unambiguous mapping between domain and codomain What I find confusing is the case when f(X) is an injective function I think that this case should be equivalent to the bijective case, and that's why H(XY) shoud be

Injection Surjection Bijection

Prove That The Function F R Rightarrow R Given By Chegg Com

Please Subscribe here, thank you!!!1) = f(a 2) for some a 1;a 2 2A, then a 1 = a 2 We say that f is bijective if it is both injective and surjective De nition 2 Let f A !B A function g B !A is the inverse of f if f g = 1 B and g f = 1 A Theorem 1 Let f A !B be bijective Then f has an inverse Proof Let f A !B be bijective We will de ne a function f 1 B !A as

2

Determine Whether The Function F Z Z F X 4x Is Chegg Com

Example 11 Show F X X2 Is Neither One One Nor Onto Examples

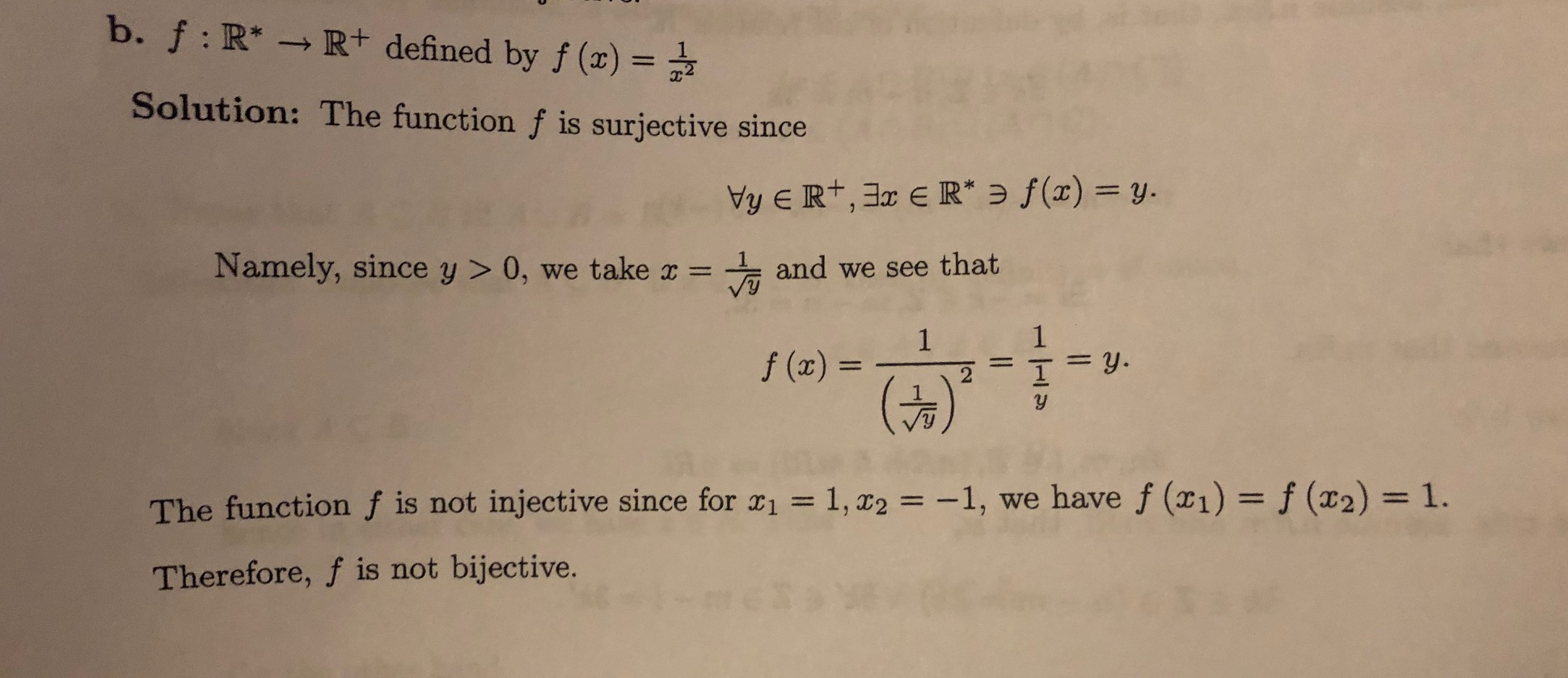
B F R R Defined By F X Solution The Function F Chegg Com

Faculty Math Illinois Edu Rdeville Teaching 347 Hw4s Pdf

Surjective Function Wikipedia

Answered 1 Let F R R Be Defined By F X 2x Bartleby

The Function F Rvec 1 2 1 2 Defined As F X X 1 X 2 Is Surjective But Not Injective 2 Neither Injective Not Surjective Invertible 4 Injective But Not Surjective

Ex 1 2 2 I Check The Injectivity And Surjectivity Of F N N

Example 11 Show F X X2 Is Neither One One Nor Onto Examples

The Function F R 1 2 1 2 Define As F X X 1 X 2 Is Sarthaks Econnect Largest Online Education Community

Check The Injectivity And Surjectivity Of The Following Functions I F N N Given By Youtube

Math Msu Edu Classes Mth 299 Mth 299 Waiver Example Problems Pdf

Ex 1 2 10 F X X 2 X 3 Is F One One Onto Class 12

Injective Surjective Mathematics Stack Exchange

State Whether The Function Is One One Onto Or Bijective F R R Defined By F X 1 X2 Brainly In

1

Function Discrete Mathematics Asst Prof Dr Choopan Rattanapoka Ppt Download

12 Onto State Whether The Function F Is Bijective Just Math

Prove That The Function F Nvecn Defined By F X X 2 X 1 Is One One But Not Onto

If A Function F 2 Infinity B Defined By F X X 2 4x 5 Is A Bijection Then B 0bq55buu Mathematics Topperlearning Com

How To Prove That F X X Sqrt X 2 1 Is Injective Quora

Classify F R R Defined By F X X X 2 1 As Injection Surjection Or Bijection

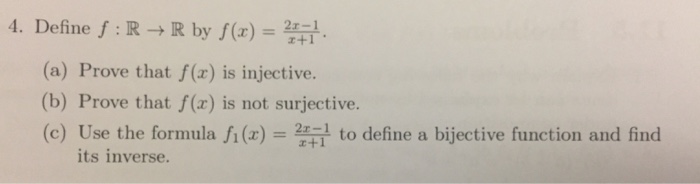
Define F R Rightarrow R By F X 2x 1 X 1 A Chegg Com

1

Check The Injectivity And Surjectivity Of Iii F R R F X X 2

Classify The Following Function F X Defined In Rtor As Injective Surjective Both Or None F X X 2 1 X 2

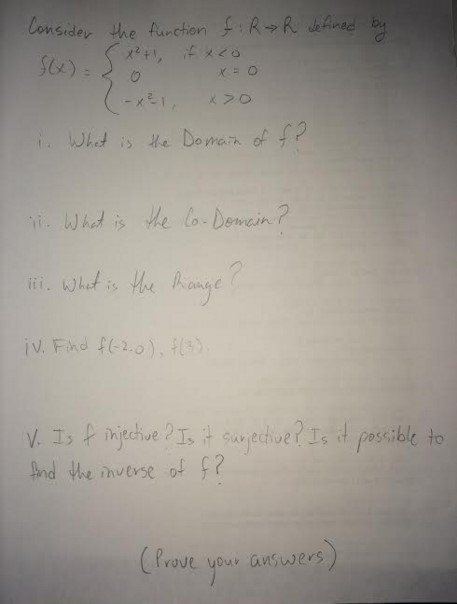
Consider The Function F R Gt R Defined By F X Chegg Com

Functions Section 2 3 Of Rosen Fall 10

Www Whitman Edu Mathematics Calculus Late Calculus Late 09 Transcendental Functions 2up Pdf

Let F Z Q F X X 2x 1 X Z Then Practice Set Gate Overflow

How Do We Prove That F 1 F X X F F 1 X X And Is It True For All Functions Quora

Injective Surjective And Bijective

Ex 1 2 2 Ii Ex 1 2

Problem 1 Determine Whether Each Of These Functions Chegg Com

Injection Surjection Bijection

Show That The Function F R R Defined By F X X X 2 1 X R Is Neither One One Nor Onto Sarthaks Econnect Largest Online Education Community

Question 4 Determine Whether Each Of These Functions Chegg Com

State Whether The Function F R R Defined By F X 1 X 2 Is One One Onto Or Bijective

1

5 5 Injective And Surjective Functions Dynamic Slides

Show That The Function F Rvec Given By F X X 3 X Is A Bijection Youtube

Classify The Following Function F X Defined In Rtor As Inj

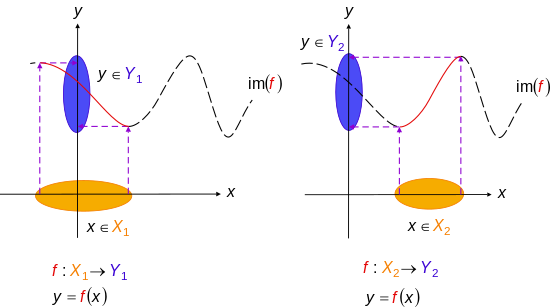
Injective Function Wikipedia

Bijection Wikipedia

Example 8 Show F X 2x Is One One But Not Onto Examples

Example 9 Prove That F X 2x Is One One And Onto Chapter 1

Q Tbn And9gcq3k4crna5aowbckdwotcepc7srb Ubkhdcqsvwzwhqp8plminb Usqp Cau

1 For Each Of The Following Functions Determine Chegg Com

Bijection Function F X Y X Y 1 2x 2y 2 Mathematics Stack Exchange

If The Function F R 1 1 To A Definded By F X X 2 1 X 2 Is Surjective Youtube

Is Function Of F X X 2 1 X 1 Continuous At X 1 Quora

1 Cmsc 250 Chapter 7 Functions 2 Cmsc 250 Function Terminology L A Relationship Between Elements Of Two Sets Such That No Element Of The First Set Is Ppt Download

Ex 1 2 2 I Check The Injectivity And Surjectivity Of F N N

Ex 1 2 10 F X X 2 X 3 Is F One One Onto Class 12

The Function F R 1 2 1 2 Defined As F X X 1 X 2 Is

Surjective Onto And Injective One To One Functions Video Khan Academy

Let F R Rightarrow R Be Given By F X X 2 1 Chegg Com

Prove The Function F Z X Z Z Given By F M N 2m N Is Onto Surjective Youtube

Part B Set Theory What Is A Set A Set Is A Collection Of Objects Can You Give Me Some Examples Ppt Download

Classify Each Function As Injective Surjective Chegg Com

Surjective Function Wikipedia

How To Prove That F X X 1 X 2 Function Is Bijective Quora

Is F X 2x 1 Is Injective Or Surjective Quora

The Function F R R Given By F X X 3 1 Is

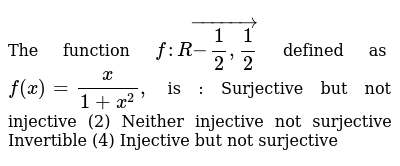
The Function F Rvec 1 2 1 2 Defined As F X X 1 X 2 Is Surjective But Not Injective 2 Neither Injective Not Surjective Invertible 4 Injective But Not Surjective

Example 11 Show F X X2 Is Neither One One Nor Onto Examples

F X 3x 4 Injective And Surjective Mathematics Stack Exchange

You Know From Calculus That Functions Play A Fundamental Role In Mathematics Pdf Free Download

The Function F R Gt 1 2 1 2 Defined As F X X 1 X 2 Is Youtube

The Function F R R F X X 2 Is A Injective But Not Surjective B Surjective But Not Injective C Injective As Well As Surjective D Neither Injective Nor Surjective

Q 16 Classify The Following Functions F X Defined In Rrarrr As Injective Surjective Both O Youtube

If A Function F R To R Is Defined As F X X 2 1 Then Youtube

State Which Of The Following Are One One And Onto Function F R Gtr Defined By F X 2x 1 Youtube

Problem 5 Determine Whether Each Of The Following Function Is Injective And Or Surjective A F Homeworklib

Question 13 Determine Whether Each Of These Chegg Com

Vatrix Match Type Question Column I 12 F R R Defined By F X X 113 F

Check The Injectivity And Surjectivity Of The Following Functions I F N N Given By F X X2 Cbse Class 12 Maths Learn Cbse Forum

Misc 5 Show F X X3 Is Injective Chapter 1 Class 12 Cbse

Let F Be A Function Defined By F X X 1 2 1 Xge1 Statement 1 The Set X F X F Youtube

Incoming Term: f(x)=x^2+1 is bijective,